数の分類について

数の種類

数にはいろいろな種類があります。日常生活で使う数だけでなく、数学の中にはさまざまな特性を持つ数が存在しているのです。今回は、これらの数の分類について簡単にみていきましょう。

実数

実数とは「実在するすべての数」のことです。

Ex.）\(２\)，\(\frac{4}{3}\)，\(\sqrt{3}\)，\(－5.12\)，\(\pi\)

私たちが日常生活においてよく使う数や、円の計算に必要な\(\pi\)(円周率)も実数の1つです。
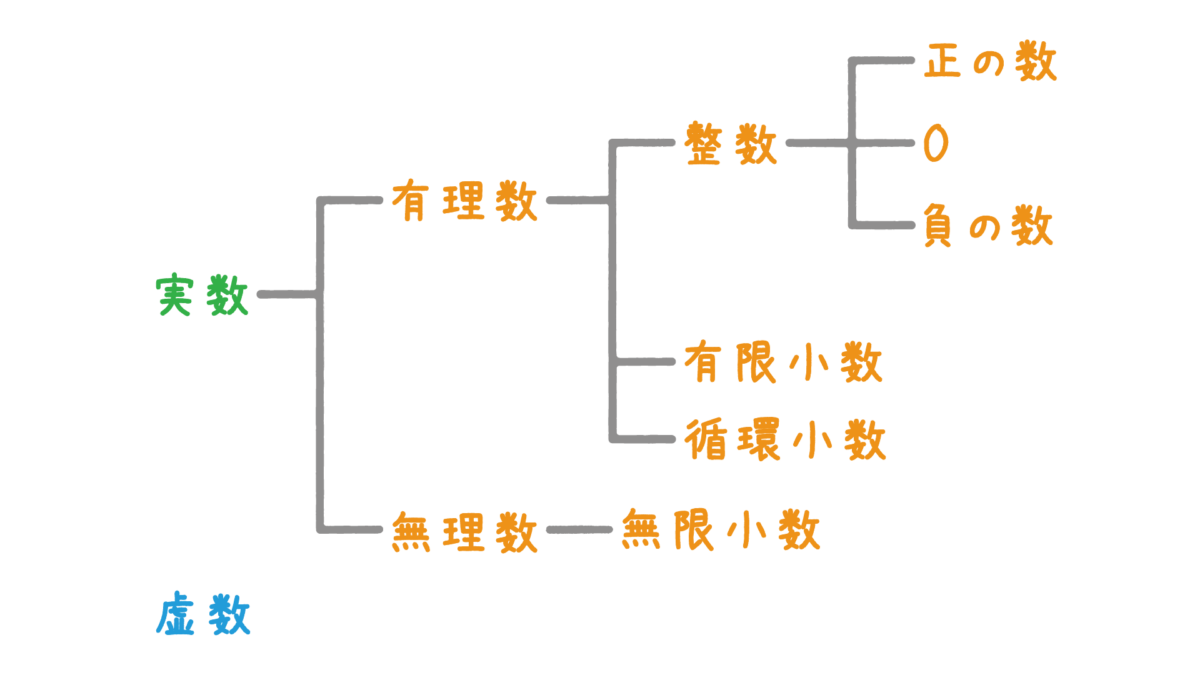
実数は「有理数」と「無理数」というカテゴリに分かれており、さらに細分化されています。
つまり、実数とは「有理数と無理数を合わせた数」とも言えますね。

有理数

有理数とは「分数で表せる数」のことです。

Ex.）\(3\)，\(\frac{7}{5}\)，\(-\frac{2}{3}\)，\(0.75\)，\(\frac{12}{99}\)(\(0.121212\ldots\))

整数や小数がこれに含まれます。
整数なのに分数というと、少し違和感を覚える方もいるかも知れません。
実際に数字を使って考えてみましょう。
\(2\)は整数ですが、\(\frac{2}{1}\)と表現できますし、\(\frac{6}{2}\)は約分すると\(\frac{3}{1}\)となり\(3\)と表せます。

また、\(\frac{1}{2}\)は\(0.5\)となり、小数となります。

整数

整数とは、小数部分を持たない数のことです。

Ex.）\(0\)，\(\pm1\)，\(\pm2\)，\(\pm3\)

日常生活でよく使う数はほとんどが整数といえますね。
整数をさらに分けると「正の数」「０」「負の数」の3つに分類できます

有限小数

有限小数とは「終わりのある小数」のことです。

Ex.）\(0.4\)(\(\frac{2}{5}\))，\(2.58\)，\(-0.001\)，\(6.123\)，\(0.995\)

このように、小数点以下が有限である数(終わりのある数)のことをいいます。

循環小数

循環小数とは「一部または全体が繰り返しのパターンを持つ小数」のことです。 

Ex.）\(\frac{1}{3}\)(\(0.33333\)…)，\(\dfrac{5}{12}\)(\(0.41666\)…)，\(\dfrac{11}{3}\)(\(0.272727\)…) 

数字の上に・（ドット）をつけて表します。 
\(0.\dot{3}\)は\(0.33333\)…と続く循環小数であり、 
\(0.\dot{2}\dot{7}\)は\(0.272727\)…と続く循環小数になります。 

無理数（無限小数）

無理数とは「分数で表すことができない数」のことです。

EX.）\(\pi\)(円周率)，\(\exp\)(ネイピア数)，\(\sqrt{2}\)(\(1.1421356\)…)，黄金比(\(1.61803398\)…)

このように無限に続く小数(終わりのない数)は無理数といえます。

虚数

虚数とは簡単に言うと「2乗すると－１になる数」のことを言います。
少し難しいですが、「実数ではない複素数」のことです。
\(i\)を使って表現します。

\(i=\sqrt{-i}\)，
\(i^{2}=-1\)

\(i\)は虚数単位と言い、「Imaginary Number」想像上の数と呼ばれます。
複素数は高校数学で学習します。