素数と素因数分解

素数は「\(1\)と自分自身でしか割り切れない、\(1\)より大きい整数」
素因数分解は「ある整数を素数の積で表すこと」
→割り切れなくなるまで小さい素数から順番に割っていく

素数
素因数分解
素因数分解のやり方
Practice

素数

素数とは「\(1\)」と「その数(自分自身)」でしか割り切れない自然数のことをいいます。

Ex.）\(2\)，\(3\)，\(5\)，\(7\)，\(9\)，\(11\)，\(13\)，\(17\)，\(19\) …

これらの数は\(１\)とその数自身でしか割ることができません。
このような数が素数です。素数は無限に存在することが知られています。

ある程度覚えておくと、次の素因数分解に役立ちます！

覚え方

兄さん（\(2\)，\(3\)）５時に（\(5\)）セブンイレブン（\(7\)，\(11\)）
父さん（\(13\)）いいなと（\(17\)）ついていく（\(19\)）

素因数分解

素因数分解とは、素数(素因数)の積で表すことをいいます。
次の数を素因数分解してみましょう。

\(12=2\times 2\times3\)

\(12\)は素数「\(2\)」と「\(3\)」の積で表すことができます。
これが素因数分解です。
このこのとき、かけている数「\(2\)」「\(2\)」「\(3\)」のことを素因数といいます。

では、
\(12=4\times 3\)
これは素因数分解といえるでしょうか？
「\(4\)」は「\(1\)と\(4\)」以外に「\(2\)と\(2\)」をかけて求めることがでるため、素数ではありません。
よって素因数分解した形とはいえませんね。
「4」を「\(2\times 2\)」に分解する必要があります。

素因数分解のやり方

素因数分解は、与えられた数を素数で順番に割っていきます。

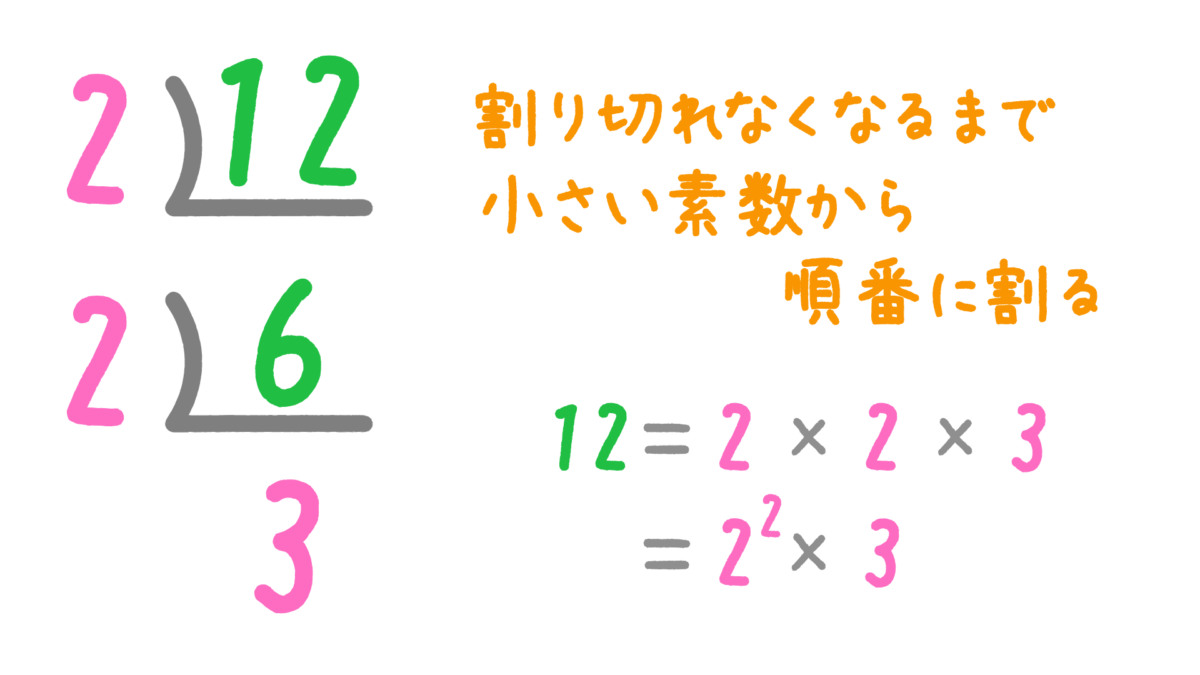
割り切れなくまで、小さい素数から順番に割っていきましょう。
割った結果が素数になるまで繰り返します。

今回の例でいうと、3は素数でありそれ以上割ることができないのでここで終了です。
\(12=2\times2\times3=2^2\times3\)
割った数を素数の掛け算の形にして表します。
同じ数字がある場合は、指数を使ってまとめましょう。

これで素因数分解ができますね。
指数については前回の記事を参考にしてください！

Practice

問．次の数を素因数分解してみましょう
（１）\(24\)
（２）\(56\)
（３）\(81\)
（４）\(36\)
（５）\(45\)
（６）\(126\)

答えを見る

（１）\(24=2\times 2\times 2\times 3=2^{3}\times 3\)
（２）\(56=2\times 2\times 2\times 7=2^{3}\times 7\)
（３）\(81=3\times 3\times 3\times 3=3^{4}\)
（４）\(36=2\times 2\times 3\times 3=2^{2}\times 3^{2}\)
（５）\(45=3\times 3\times 5=3^{2}\times 5\)
（６）\(126=2\times 3\times 3\times 7=2\times 3^{2}\times 7\)