数の大小と不等号

数直線

数直線を使って数の大小(正の数、負の数)を視覚的に表してみます。

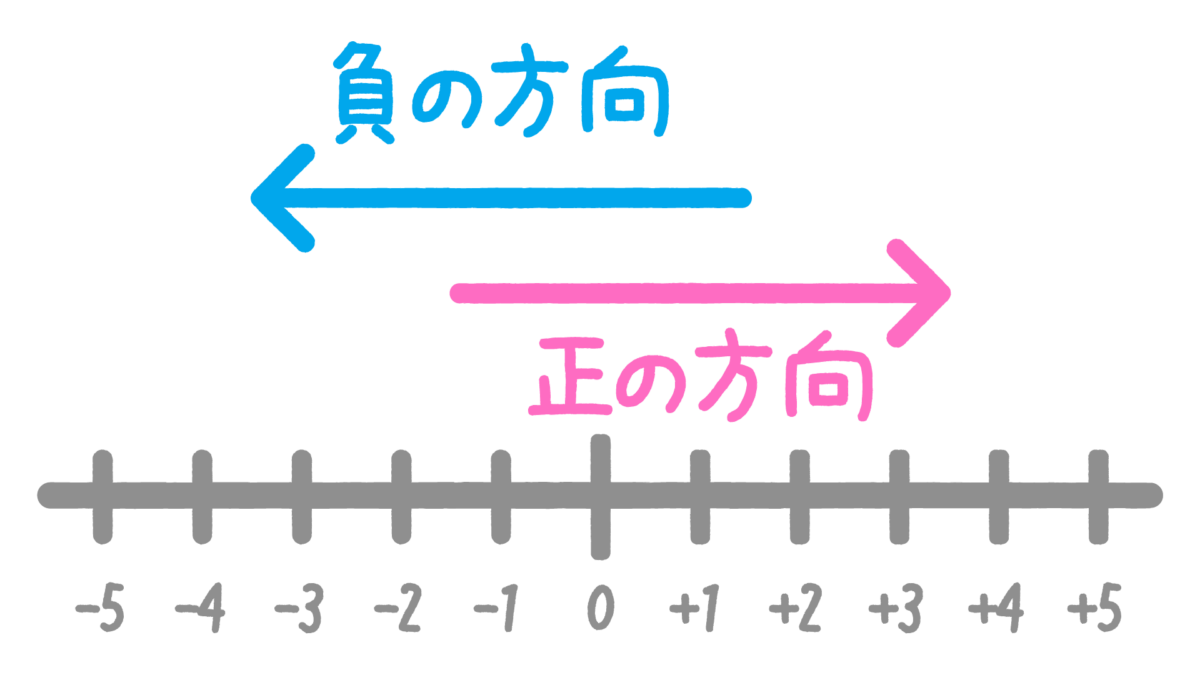
数直線上に基準となる点を0(原点)として決め、この点から等間隔に数を並べていきます。このとき、数直線の右の方向を「正の方向」、左側の方向を「負の方向」といいます。

不等号(\(<，>，\leqq， \geqq\))

不等号とは数の大小関係を表す記号です。
どちらの数が大きいかを表します。
主に、次の4種類がああります。

• 「\(<\)」…小なり
• 「\(>\)」…大なり
• 「\(\leqq\)」…小なりイコール
• 「\(\geqq\)」…大なりイコール

不等号の口が開いている方が大きな数となります。
=がついた不等号は等しい関係も含むことを意味します。
それぞれ詳しく見ていきましょう！

A\(<\)B(A小なりB)

この場合、「AはBより小さい」ことを意味し、
「AはB未満」とも言えます。

A\(>\)B(A大なりB)

この場合、「AはBよりも大きい」ことを意味します。

A\(\leqq\)B(A小なりイコールB)

この場合、「AはBよりも小さい、または等しい」ことを意味し、
「AはB以下」とも言えます。
イコールがついてる不等号なので、等しい関係も含みますね。

A\(\geqq\)B(A大なりイコールB)

この場合、「AはBよりも大きい、または等しい」ことを意味し、
「AはB以上」とも言えます。
これもイコールがついてい不等号なので、等しい関係も含みますね。

Practice

問１．数直線上において、０に対応する点は何というでしょう。

答えを見る”閉じる”

問２．数直線上において、右の方向、左の方向をそれぞれ何というでしょう。

答えを見る”閉じる”

問３．\(\Box\)に入る不等号を答えてみましょう。
（１）\(3\Box5\)
（２）\(10\Box-3\)
（３）\(-2\Box-5\)
（４）\(\frac{2}{7}\Box\frac{5}{7}\)
（５）\(\frac{1}{3}\Box\frac{1}{5}\)

答えを見る”閉じる”

問４．次の数の大小関係を答えてみましょう。
（１）Aは\(5\)より大きい
（２）Bは\(-2\)以上である
（３）Cは\(5\)以下である
（４）Dは\(3\)未満である

答えを見る”閉じる”